Introduction of Point-Slope Form With Definition, Derivation, and Examples
The point-slope form is used to determine the equation of a straight line. By using the slope and given point, we can easily find the equation of a straight line. Point-slope form deals with linear equations only. In a linear equation, the degree (power) of the unknown variables is one.
There are four following methods used to find the equation of a straight line by using different parameters.
- Point-slope form
- Intercept form
- Slope-intercept form
- Two-point form
In this article, we will confine ourselves only point-slope form with its formula. We will discuss how to derive the equation of the point-slope. We will learn how to calculate the equation of a line by using point-slope form. Further, we will solve some examples with a step-by-step solution.
What is Point-Slope Form?
The point-slope form is an equation of the straight line that passes through the given coordinate (x1, y1) and has a slope of line “m”. Mathematically, the equation of point-slope form is written as,
| (y – y1) = m (x – x1) | Here,
|
We can find the equation of point-slope form when the slope and at least one point on the line are given.
Derive the equation of point-slope form
We can derive the equation of point-slope form by using the definition of the slope. Suppose the line passes through the given point (x1, y1), and (x, y) is any other point on the line. Then the slope of the line is defined as the ratio between the rate of change in y and the rate of change in x.
Slope = m = rate of change in y / rate of change in x
Slope = m = (y – y1) / (x – x1)
Multiply (x – x1) on both sides and by arranging the above equation, we get
(y – y1) = m (x – x1)
That is the equation of point-slope form.
Method to determine the equation of point-slope form
- Write down the slope and given point of the straight line.
- Put the given values in the equation of point-slope form that is (y – y1) = m (x – x1)
- Simplify the equation until it changes in a general form.
Some important Results of point-slope form
- If the line passes through the point (x1, y1), and has slope m, then the equation of point-slope form is
(y – y1) = m (x – x1)
- If the straight line passes through (a, b) horizontally, or in other words line passes through the y-axis, then it gives y1 = b, and we know that on the y-axis, x is always zero. So, x1 = 0. i.e. (x1, y1) = (0, b), and the equation of point-slope form becomes,
(y – b) = m (x – 0)
y – b = m x
y = m x + b
it is called the equation of the slope-intercept form.
- If the line passes through (a, b) vertically, or the line passes through the x-axis, then it gives x1 = a, y1 = 0 because on the x-axis y is always zero. i.e. (x1, y1) = (a, 0), then the equation of point-slope form will be,
(y – 0) = m (x – a)
y = m (x – a)
- If the straight line passes through the origin in this case (x1, y1) = (0, 0), i.e
(y – 0) = m (x – 0)
y = mx
Example of Point-sope form
To understand the point-slope form, let’s solve some examples.
Example 1.
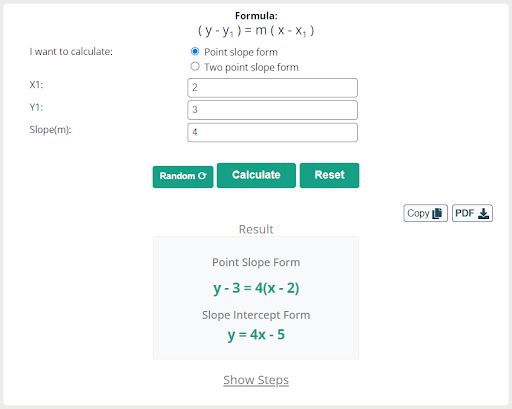
Find the equation of a straight line when the line passes through the point (2, 3), and has slope 4.
Solution
Step 1. Note the given point and slope. Here
(x1, y1) = (2, 3)
m = 4
Step 2. Given data put in the equation of the point-slope form, i.e. (y – y1) = m (x – x1), we get
(y – 3) = 4 (x – 2)
Step 3. Simplify the above equation
y – 3 = 4x – 8
y = 4x – 8 + 3
y = 4x – 5
You can try a point slope form calculator by Allmath to evaluate the problems of line equations by using the slope and coordinate points of the line.
Example 2.
A line passes through a point (4, 7) that has a slope 2 / 3. Find the equation of a line by using the point-slope form equation.
Solution
In this example we have (x1, y1) = (4, 7) and m = 2 / 3
We know that the point-slope form equation (y – y1) = m (x – x1), now put the given value in this equation.
(y – 7) = (2 / 3) (x – 4)
3 multiply both sides, we get,
3y – 21 = 2(x – 4)
3y – 21 = 2x – 8
3y = 2x – 8 + 21
3y = 2x + 13
By dividing 3 each term,
y = (2 / 3) x + (13 / 3)
Hence, it is a required equation of a line.
Summary
In this article, we learn when we use point-slope form. We have discussed the definition of slope-point form with its formula. All terms related to point-slope form are covered in this article. Then we derived the equation of point-slope form. We learn how to find the equation of a straight line by using point-slope form.
We discussed some important results of point-slope form in this article. Further, we solved some examples to find the equation of a straight line. After reading this article, you will be able to find the equation of the line by using the equation of point slope form.








